[WIP] The Elements of Computing Systems – Building a Modern Computer from First Principles

Chapter 1: Boolean logic

Modern computers store and process information stored as two-valued signals — called bits (i.e. binary digits). Two-value signals were chosen because they can readily be represented, stored, and transmitted. For example, they can be represented as:

A binary variable or a bit can represent two possible states: 0 and 1; off and on; false and true; no and yes; etc. nn binary variables can be used to represent 2n2^n states. e.g.

b2b_2 b1b_1 b0b_0
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

Boolean algebra is used to manipulate binary values. A boolean function (aka boolean operator) is a function that operates on binary inputs and returns binary outputs.

The total number of boolean functions for nn binary variables is 22n2^{2^n}, because:

e.g. There are 1616 distinct boolean functions for 22 binary variables.

Function Expression A=0, B=0 A=0, B=1 A=1, B=0 A=1, B=1
F0 0 0 0 0 0
F1 NOT A AND NOT B 1 0 0 0
F2 NOT A AND B 0 1 0 0
F3 NOT A 1 1 0 0
F4 A AND NOT B 0 0 1 0
F5 NOT B 1 0 1 0
F6 XOR(A, B) 0 1 1 0
F7 NAND(A, B) 1 1 1 0
F8 A AND B 0 0 0 1
F9 XNOR(A, B) 1 0 0 1
F10 B 0 1 0 1
F11 NOT A OR B 1 1 0 1
F12 A 0 0 1 1
F13 A OR NOT B 1 0 1 1
F14 A OR B 0 1 1 1
F15 1 1 1 1 1

A logic gate (also called chip in the book) is a physical device that implements a boolean function. Every digital device is based on a set of chips designed to store and process binary information. These chips are all made of elementary logic gates. Elementary logic gates can be physically realized using many different hardware technologies, but their logical behavior, or abstraction, is consistent across implementations.

Since all logic gates have the same input and output data type (i.e. binary), they can be combined, creating composite gates of arbitrary complexity. e.g. Xor = Or(And(a, Not(b)), And(Not(a), b)).

Any given logic gate can be viewed from two perspective:

  1. External: The interface of the gate, outlining its input pins, output pins, and its behavior.
  2. Internal: The implementation of the gate. There can be multiple implementations of a gate’s interface. The goal is to find an implementation that is correct (functional requirement) and efficient (performance requirement).

A hardware description language (HDL) is a specialized computer language used to describe the structure and behavior of chips.

The designer specifies the chip logic by writing a HDL program, which is then subjected to a rigorous battery of tests. The tests are carried out virtually, using computer simulation: A special software tool, called a hardware simulator, takes the HDL program as input and creates a software representation of the chip logic. Next, the designer can instruct the simulator to test the virtual chip on various sets of inputs. The simulator computes the chip outputs, which are then compared to the desired outputs.

The hardware simulator can also simulate and quantify the performance characteristics (energy consumption, computational speed, cost) of a chip.

The specifications of the logic gates needed to build the chips of our computer system are given below.

First, the primitive NAND gate, which is shorthand for Not-And because it’s equivalent to Not(And(a, b)).

Truth table:

a b Nand(a, b)
0 0 1
0 1 1
1 0 1
1 1 0

API:
Chip name Nand
Input a, b
Output out
Function if ((a == 1) and (b==1)) then out = 0, else out = 1

The NAND gate is called a primitive gate because it can be used to implement any boolean function. Proof:

Next, we look at a set of four gates that implement classical logical operators. Starting with the Not (aka inverter) gate, which outputs the opposite value of its input’s value.

Truth table:

a Not(a)
0 1
1 0

API:
Chip name Not
Input in
Output out
Function if (in == 0) then out = 1, else out = 0

HDL:


CHIP Not {

IN in;

OUT out;

  

PARTS:

Nand(a= in, b= in, out= out);

}

The next classical gate is the AND gate, which returns 11 when both its inputs are 11, and 00 otherwise.

Truth table:

a b And(a, b)
0 0 0
0 1 0
1 0 0
1 1 1

API:
Chip name And
Input a, b
Output out
Function if ((a == 1) and (b==1)) then out = 1, else out = 0

HDL:


CHIP And {

IN a, b;

OUT out;

PARTS:

Nand(a= a, b= b, out= nandout);

Not(in= nandout, out= out);

}

The Or gate returns 11 when at least one of its inputs is 11, and 00 otherwise.

Truth table:

a b Or(a, b)
0 0 0
0 1 1
1 0 1
1 1 1

API:
Chip name Or
Input a, b
Output out
Function if ((a == 0) and (b == 0)) then out = 0, else out = 1

HDL:


CHIP Or {

IN a, b;

OUT out;

  

PARTS:

Not(in= a, out= nota);

Not(in= b, out= notb);

And(a= nota, b= notb, out= notaandnotb);

Not(in= notaandnotb, out= out);

}

The last classical gate we will build is the Xor (aka exclusive or) gate which returns 11 when exactly one of its input is 11, and 00 otherwise.

Truth table:

a b Xor(a, b)
0 0 0
0 1 1
1 0 1
1 1 0

API:
Chip name Xor
Input a, b
Output out
Function if (a != b) then out = 1, else out = 0

HDL:


CHIP Xor {

IN a, b;

OUT out;

  

PARTS:

Not(in= a, out= nota);

Not(in= b, out= notb);

And(a= a, b= notb, out= aandnotb);

And(a= b, b= nota, out= bandnota);

Or(a= aandnotb, b= bandnota, out= out);

}

Next, we look at a set of control flow gates. These gates provide means for controlling flows of information. The first of such gate is the multiplexer which is a three-input gate. Two input bits, named a and b, are interpreted as data bits, and a third bit, named sel, is interpreted as a selection bit. The multiplexer uses sel to select and output the value of either a or b.

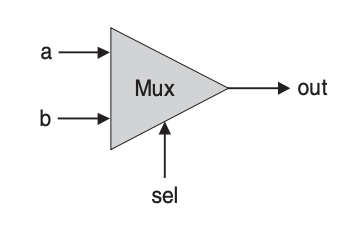
Truth table:

a b sel out
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 1

API:
Chip name Mux
Input a, b, sel
Output out
Function if (sel == 0) then out = a, else out = b

HDL:


CHIP Mux {

IN a, b, sel;

OUT out;

  

PARTS:

Not(in= sel, out= notsel);

And(a= a, b= notsel, out= aandnotsel);

And(a= b, b= sel, out= bandsel);

Or(a= aandnotsel, b= bandsel, out= out);

}

Next is the demultiplexer gate which performs the opposite function of a multiplexer: it takes a single input value and routes it to one of two possible outputs, according to a selector bit that selects the destination output.

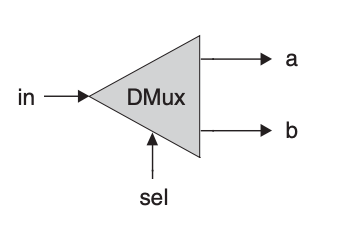
in sel a b
0 0 0 0
0 1 0 0
1 0 1 0
1 1 0 1

API:
Chip name DMux
Input in, sel
Output a, b
Function if (sel == 0) then {a, b} = {in, 0}, else {a, b} = {0, in}

HDL:


CHIP DMux {

IN in, sel;

OUT a, b;

  

PARTS:

Not(in= sel, out= notsel);

And(a= in, b= notsel, out= a);

And(a= in, b= sel, out= b);

}

Now, we explore multi-bit versions of some of the basic gates above. This section describes several 16-bit logic gates that will be needed for constructing our target computer platform. HDL programs treat multi-bit values like single-bit values, except that the values can be indexed in order to access individual bits. For example, if in and out represent 16-bit values, then out [3] = in[5] sets the 3rd bit of out to the value of the 5th bit of in. The bits are indexed from right to left, the rightmost bit being the 0’th bit and the leftmost bit being the 15’th bit (in a 16-bit setting).

The first multi-bit gate we will build is the 16-bit Not gate, which applies the Boolean operation Not to every one of the input bits.

API:
Chip name Not16
Input in[16]
Output out[16]
Function for i = 0..15 out[i] = Not(in[i])

HDL:


CHIP Not16 {

IN in[16];

OUT out[16];

  

PARTS:

Not(in= in[0], out= out[0]);

Not(in= in[1], out= out[1]);

Not(in= in[2], out= out[2]);

Not(in= in[3], out= out[3]);

Not(in= in[4], out= out[4]);

Not(in= in[5], out= out[5]);

Not(in= in[6], out= out[6]);

Not(in= in[7], out= out[7]);

Not(in= in[8], out= out[8]);

Not(in= in[9], out= out[9]);

Not(in= in[10], out= out[10]);

Not(in= in[11], out= out[11]);

Not(in= in[12], out= out[12]);

Not(in= in[13], out= out[13]);

Not(in= in[14], out= out[14]);

Not(in= in[15], out= out[15]);

}

Next is the 16-bit And gate, which applies the Boolean operation And to every one of the input bits.

API:
Chip name And16
Input a[16], b[16]
Output out[16]
Function for i = 0..15 out[i] = And(a[i], b[i])

HDL:


CHIP And16 {

IN a[16], b[16];

OUT out[16];

  

PARTS:

And(a= a[0], b= b[0], out= out[0]);

And(a= a[1], b= b[1], out= out[1]);

And(a= a[2], b= b[2], out= out[2]);

And(a= a[3], b= b[3], out= out[3]);

And(a= a[4], b= b[4], out= out[4]);

And(a= a[5], b= b[5], out= out[5]);

And(a= a[6], b= b[6], out= out[6]);

And(a= a[7], b= b[7], out= out[7]);

And(a= a[8], b= b[8], out= out[8]);

And(a= a[9], b= b[9], out= out[9]);

And(a= a[10], b= b[10], out= out[10]);

And(a= a[11], b= b[11], out= out[11]);

And(a= a[12], b= b[12], out= out[12]);

And(a= a[13], b= b[13], out= out[13]);

And(a= a[14], b= b[14], out= out[14]);

And(a= a[15], b= b[15], out= out[15]);

}

Followed by the 16-bit Or gate, which applies the Boolean operation Or to every one of the input bits.

API:
Chip name Or16
Input a[16], b[16]
Output out[16]
Function for i = 0..15 out[i] = Or(a[i], b[i])

HDL:


CHIP Or16 {

IN a[16], b[16];

OUT out[16];

  

PARTS:

Or(a= a[0], b= b[0], out= out[0]);

Or(a= a[1], b= b[1], out= out[1]);

Or(a= a[2], b= b[2], out= out[2]);

Or(a= a[3], b= b[3], out= out[3]);

Or(a= a[4], b= b[4], out= out[4]);

Or(a= a[5], b= b[5], out= out[5]);

Or(a= a[6], b= b[6], out= out[6]);

Or(a= a[7], b= b[7], out= out[7]);

Or(a= a[8], b= b[8], out= out[8]);

Or(a= a[9], b= b[9], out= out[9]);

Or(a= a[10], b= b[10], out= out[10]);

Or(a= a[11], b= b[11], out= out[11]);

Or(a= a[12], b= b[12], out= out[12]);

Or(a= a[13], b= b[13], out= out[13]);

Or(a= a[14], b= b[14], out= out[14]);

Or(a= a[15], b= b[15], out= out[15]);

}

Finally, the 16-bit Multiplexer gate, which operates exactly as the basic multiplexer, except that its input and output are 16-bits wide.

API:
Chip name Mux16
Input a[16], b[16], sel
Output out[16]
Function if (sel == 0) then for i = 0..15 out[i] = a[i], else for i = 0..15 out[i] = b[i]

HDL:


CHIP Mux16 {

IN a[16], b[16], sel;

OUT out[16];

  

PARTS:

Mux(a= a[0], b= b[0], sel= sel, out= out[0]);

Mux(a= a[1], b= b[1], sel= sel, out= out[1]);

Mux(a= a[2], b= b[2], sel= sel, out= out[2]);

Mux(a= a[3], b= b[3], sel= sel, out= out[3]);

Mux(a= a[4], b= b[4], sel= sel, out= out[4]);

Mux(a= a[5], b= b[5], sel= sel, out= out[5]);

Mux(a= a[6], b= b[6], sel= sel, out= out[6]);

Mux(a= a[7], b= b[7], sel= sel, out= out[7]);

Mux(a= a[8], b= b[8], sel= sel, out= out[8]);

Mux(a= a[9], b= b[9], sel= sel, out= out[9]);

Mux(a= a[10], b= b[10], sel= sel, out= out[10]);

Mux(a= a[11], b= b[11], sel= sel, out= out[11]);

Mux(a= a[12], b= b[12], sel= sel, out= out[12]);

Mux(a= a[13], b= b[13], sel= sel, out= out[13]);

Mux(a= a[14], b= b[14], sel= sel, out= out[14]);

Mux(a= a[15], b= b[15], sel= sel, out= out[15]);

}

The last set of gates we will build are the multi-way versions of basic gates. Logic gates that operate on one or two inputs have natural generalization to multi-way variants that operate on more than two inputs.

The first gate in this set is the multi-way Or gate. An $m$-way Or gate outputs 1 when at least one of its m input bits is 1, and 0 otherwise. Our target computer will need an $8$-way variant of this gate:
Chip name Or8Way
Input in[8]
Output out
Function out = Or(in[0], in[1], ..., in[7]) 
CHIP Or8Way {

IN in[8];

OUT out;

  

PARTS:

Or(a= in[0], b= in[1], out= in01);

Or(a= in01, b= in[2], out= in012);

Or(a= in012, b= in[3], out= in0123);

Or(a= in0123, b= in[4], out= in01234);

Or(a= in01234, b= in[5], out= in012345);

Or(a= in012345, b= in[6], out= in0123456);

Or(a= in0123456, b= in[7], out= out);

}

Next, we build a multi-way multi-bit multiplexer gate. An m$-way $n$-bit multiplexer selects one of its $m n$-bit inputs, and outputs it to its $n$-bit output. The selection is specified by a set of $k selection bits, where k=log2mk = log_2{m}.

Our target computer platform requires two variants of this chip: a $4$-way $16$-bit multiplexer and an $8$-way $16$-bit multiplexer.

API:
Chip name Mux4Way16
Input a[16], b[16], c[16], d[16], sel[2]
Output out[16]
Function if (sel == 00) then out = a,

else if (sel == 01) then out = b,

else if (sel == 10) then out = c,

else if (sel == 11) then out = d
Chip name Mux8Way16
Input a[16], b[16], c[16], d[16], e[16], f[16], g[16], h[16], sel[3]
Output out[16]
Function if (sel == 000) then out = a,

else if (sel == 001) then out = b,

else if (sel == 010) then out = c,

else if (sel == 011) then out = d

else if (sel == 100) then out = e,

else if (sel == 101) then out = f,

else if (sel == 110) then out = g,

else if (sel == 111) then out = h

HDL:

CHIP Mux4Way16 {

IN a[16], b[16], c[16], d[16], sel[2];

OUT out[16];

PARTS:

// First level: Select between a/b and c/d using sel[0]

Mux16(a=a, b=b, sel=sel[0], out=ab); // ab is the output of first Mux16

Mux16(a=c, b=d, sel=sel[0], out=cd); // cd is the output of second Mux16

  

// Second level: Select between ab and cd using sel[1]

Mux16(a=ab, b=cd, sel=sel[1], out=out);

}

CHIP Mux8Way16 {

IN a[16], b[16], c[16], d[16],

e[16], f[16], g[16], h[16],

sel[3];

OUT out[16];

  

PARTS:

Mux4Way16(a= a, b= b, c= c, d= d, sel= sel[0..1], out= abcd);

Mux4Way16(a= e, b= f, c= g, d= h, sel= sel[0..1], out= efgh);

Mux16(a= abcd, b= efgh, sel= sel[2], out= out);

}

Finally, we build a multi-way 16-bit demultiplexer gate. An m$-way $n$-bit demultiplexer routes its single $n$-bit input to one of its $m n$-bit outputs. The other outputs are set to `0`. The selection is specified by a set of $k selection bits, where k=log2mk = log_2{m}.

Our target computer platform requires two variants of this chip: a $4$-way $1$-bit demultiplexer and an $8$-way $1$-bit demultiplexer.

API:
Chip name DMux4Way
Input in, sel[2]
Output a, b, c, d
Function if (sel == 00) then {a, b, c, d} = {in, 0, 0, 0},

else if (sel == 01) then {a, b, c, d} = {0, in, 0, 0},

else if (sel == 10) then {a, b, c, d} = {0, 0, in, 0},

else if (sel == 11) then {a, b, c, d} = {0, 0, 0, in}

HDL:

CHIP DMux4Way {

IN in, sel[2];

OUT a, b, c, d;

  

PARTS:

DMux(in= in, sel= sel[1], a= first, b= second);

DMux(in= first, sel= sel[0], a= a, b= b);

DMux(in= second, sel= sel[0], a= c, b= d);

}
Chip name DMux8Way
Input in, sel[3]
Output a, b, c, d, e, f, g, h
Function if (sel == 000) then {a, b, c, …, h} = {1, 0, 0, 0, 0, 0, 0, 0},

else if (sel == 001) then {a, b, c, …, h} = {0, 1, 0, 0, 0, 0, 0, 0},

if (sel == 010) then {a, b, c, …, h} = {0, 0, 1, 0, 0, 0, 0, 0},

…

if (sel == 111) then {a, b, c, …, h} = {0, 0, 0, 0, 0, 0, 0, 1}

HDL:

CHIP DMux8Way {

IN in, sel[3];

OUT a, b, c, d, e, f, g, h;

  

PARTS:

DMux(in= in, sel= sel[2], a= first, b= second);

DMux4Way(in= first, sel= sel[0..1], a= a, b= b, c= c, d= d);

DMux4Way(in= second, sel= sel[0..1], a= e, b= f, c= g, d= h);

}

Chapter 2: Boolean arithmetic

🎯 Objective: Use the gates from chapter 1 to build an ALU (Arithmetic logic unit).

The ALU is the centerpiece chip that executes all the arithmetic and logical operations performed by the computer.

A binary number is a number expressed in the base-2 positional numeral system. Let x=xnxn−1xn−2...x0x = x_{n}x_{n − 1}x_{n − 2} ... x_{0} be a string of binary digits, the value of xx in the base-2 positional numeral system is defined as:
$
x = \sum_{i=0}^{n} x_i \cdot b^i
$

e.g.

1001012100101_2 = [(1)×25]+[(0)×24]+[(0)×23]+[(1)×22]+[(0)×21]+[(1)×20][ ( 1 ) × 2^5 ] + [ ( 0 ) × 2^4 ] + [ ( 0 ) × 2^3 ] + [ ( 1 ) × 2^2 ] + [ ( 0 ) × 2^1 ] + [ ( 1 ) × 2^0 ]

1001012100101_2 = [1×32]+[0×16]+[0×8]+[1×4]+[0×2]+[1×1][ 1 × 32 ] + [ 0 × 16 ] + [ 0 × 8 ] + [ 1 × 4 ] + [ 0 × 2 ] + [ 1 × 1 ]

1001012100101_2 = 371037_{10}

A numeral system is a mathematical notation for representing numbers of a given set using digits or other symbols in a consistent manner.

In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers.

Computers represent numbers in binary. Any number can be represented by a sequence of bits (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states.

Integer numbers are unbounded: for any given number xx, there are integers that are less than xx and integers greater than xx. However, computers are finite machines that use a fixed word size for representing numbers. An 8-bit register can represent 28=2562^8 = 256 different things. Using nn bits, we can represent all the nonnegative integers ranging from 00 to 2n−12^n - 1.

The three common methods of extending the binary numeral system to represent signed numbers (i.e. positive, negative, and zero numbers) numbers are:

Of the three, two’s complement is the most commonly used today.

A two's complement number system encodes positive and negative numbers in a binary number representation. The weight of each bit is a power of two, except for the most significant bit (aka sign bit), whose weight is the negative of the corresponding power of two. The value ww of an N$-bit integer $a_{N-1} a_{N-2} ... a_0 is given by the following formula:

w=−(aN−12N−1)+∑i=0N−2ai2iw = -(a_{N-1} 2^{N-1}) + \sum_{i=0}^{N-2} a_i 2^i

The two's complement of an N$-bit number is the complement of that number with respect to $2^N (this is the property that gives this system its name). i.e. Given that xx is an N$-bit number and $y is its two's complement, then x+y=2Nx + y = 2^N. e.g.

N=3N = 3 2N=23=810=100022^N = 2^3 = 8_{10} = 1000_2 If x=0112 (310)If \space x = 011_2 \space (3_{10})

Then yy ($x#39;s two's complement) =1012= 101_2 (510)(5_{10}) because: $ 011_2 + 101_2 = 1000_2 = 2^N $

Calculation of the two's complement of a number essentially means subtracting the number from 2N2^N. But as can be seen from the 3-bit example above with the 4-bit 100021000_2, the number 2N2^N will not itself be representable in a system limited to NN bits, as it is just outside the NN bit space. Because of this, systems with maximally $N$-bit must break the subtraction into two operations:

  1. First, subtract from the maximum number in the N$-bit system, that is $2^N - 1. This term in binary is actually a simple number consisting of 'all 1s', and a subtraction from it can be done by simply inverting all bits in the number. The number obtained in this step is called the ones' complement because summing it with the original number yields 'all 1s'.
  2. Secondly, add one to the result.
Bits Unsigned value Signed value (Two's complement)
000 0 0
001 1 1
010 2 2
011 3 3
100 4 -4
101 5 -3
110 6 -2
111 7 -1

Here is why the two's complement system works. Given a set of all possible N$-bit values, we can assign the lower (by the binary value) half to be the integers from $0 to (2N−1−1)(2^{N-1} - 1) inclusive and the upper half to be −2N−1-2^{N-1} to −1-1 inclusive. The upper half (again, by the binary value) can be used to represent negative integers from −2N−1-2^{N-1} to −1-1 because, under addition modulo 2N2^N they behave the same way as those negative integers. That is to say that, because i+j mod 2N=i+(j+2N) mod 2Ni + j \bmod 2^N = i + (j + 2^N) \bmod 2^N, any value in the set {j+k2N ∣ k is an integer}\{j + k2^N \space | \space k \space is \space an \space integer\} can be used in place of jj. Fundamentally, the system counts negative numbers by counting backwards and wrapping around.

Given 2N=232^N = 2^3, these are some examples:

Addition in the two's complement system Addition modulo 232^3
−4+3=−1-4 + 3 = -1 (represented as 77 in binary) 4+3 mod 8=74 + 3 \bmod 8 = 7 (the two's complement representation of $-1$)
−3+3=0-3 + 3 = 0 (represented as 00 in binary) 5+3 mod 8=85 + 3 \bmod 8 = 8 (the two's complement representation of $0$)
−2+3=1-2 + 3 = 1 (represented as 11 in binary) 6+3 mod 8=16 + 3 \bmod 8 = 1 (the two's complement representation of $1$)

The two's complement system has the following advantages over other systems for representing signed numbers:

  1. The fundamental arithmetic operations of addition, subtraction, and multiplication are identical to those for unsigned binary numbers (as long as the inputs are represented in the same number of bits as the output, and any overflow beyond those bits are discarded from the result).
  2. It has no representation for negative zero (unlike the ones' complement and sign-magnitude representations).

The material implications of these theoretical results are significant:

A pair of binary numbers can be added bitwise from right to left, using the same decimal addition algorithm learned in elementary school.


1 1 1 1 1 (carried bits )

  0 1 1 0 1 (13_10)

+ 1 0 1 1 1 (23_10)

-------------

1 0 0 1 0 0 (36_10)

When adding in the two's complement system, any extra carry bit is discarded, such that the result and the addends always have the same number of bits. This is effectively the same as applying the modulo operator. For any number xx, computing x mod 2Nx \bmod 2^N essentially results in keeping the lowest NN bits of the number xx. As explained in the two's complement section, this modulo operation is what makes the two's complement system work.

An adder or summer is a digital circuit used in the ALU to perform addition on binary numbers. We saw (from the elementary school style addition) that computer hardware for binary addition of two $n$-bit numbers can be built from logic gates designed to calculate the sum of three bits (pair of bits plus carry bit). These are the following hierarchy of adders that will be built:

A half adder is designed to add two bits.
Chip name HalfAdder
Input a, b
Output sum, carry
Function sum = LSB of a + b

carry = MSB of a + b

An inspection of the truth table reveals that the outputs sum(a, b) and carry(a, b) are identical to those of two simple Boolean functions Xor and And respectively.

a b carry sum
0 0 0 0
0 1 0 1
1 0 0 1
1 1 1 0 
/**
* Computes the sum of two bits.
*/
CHIP HalfAdder {

IN a, b; // 1-bit inputs

OUT sum, // Right bit of a + b

carry; // Left bit of a + b

PARTS:

And(a= a, b= b, out= carry);

Xor(a = a, b = b, out = sum);
}

A full adder is designed to add three bits. Like the half-adder, the full-adder chip outputs two bits that, taken together, represents the addition of the three input bits.
Chip name FullAdder`
Input a, b, c
Output sum, carry
Function sum = LSB of a + b + c

carry = MSB of a + b + c
a b c carry sum
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1

The names Half-adder and Full-adder derive from the implementation detail that a full-adder chip can be realized from two half-adders (and one other basic chip).

/**
* Computes the sum of three bits.
*/

CHIP FullAdder {

IN a, b, c; // 1-bit inputs

OUT sum, // Right bit of a + b + c

carry; // Left bit of a + b + c

PARTS:

HalfAdder(a= a, b= b, sum= partialSum, carry= partialCarry);

HalfAdder(a= partialSum, b= c, sum= sum, carry= partialCarry2);

Or(a= partialCarry, b= partialCarry2, out= carry);
}

An adder is designed to add two $n$-bit numbers.
Chip name Add16
Input a[16], b[16]
Output out[16]
Function Adds two 16-bit numbers.
Comment The overflow bit is ignored.

The addition of two $n$-bit numbers can be done bitwise, from right to left (from LSB pairs to MSB pairs). In each step, the resulting carry bit from the previous step is fed into the addition.

/**
* 16-bit adder: Adds two 16-bit two's complement values.
* The most significant carry bit is ignored.
*/

CHIP Add16 {

IN a[16], b[16];

OUT out[16];

  

PARTS:

FullAdder(a= a[0], b= b[0], c= false, sum= out[0], carry= carry0);

FullAdder(a= a[1], b= b[1], c= carry0, sum= out[1], carry= carry1);

FullAdder(a= a[2], b= b[2], c= carry1, sum= out[2], carry= carry2);

FullAdder(a= a[3], b= b[3], c= carry2, sum= out[3], carry= carry3);

FullAdder(a= a[4], b= b[4], c= carry3, sum= out[4], carry= carry4);

FullAdder(a= a[5], b= b[5], c= carry4, sum= out[5], carry= carry5);

FullAdder(a= a[6], b= b[6], c= carry5, sum= out[6], carry= carry6);

FullAdder(a= a[7], b= b[7], c= carry6, sum= out[7], carry= carry7);

FullAdder(a= a[8], b= b[8], c= carry7, sum= out[8], carry= carry8);

FullAdder(a= a[9], b= b[9], c= carry8, sum= out[9], carry= carry9);

FullAdder(a= a[10], b= b[10], c= carry9, sum= out[10], carry= carry10);

FullAdder(a= a[11], b= b[11], c= carry10, sum= out[11], carry= carry11);

FullAdder(a= a[12], b= b[12], c= carry11, sum= out[12], carry= carry12);

FullAdder(a= a[13], b= b[13], c= carry12, sum= out[13], carry= carry13);

FullAdder(a= a[14], b= b[14], c= carry13, sum= out[14], carry= carry14);

FullAdder(a= a[15], b= b[15], c= carry14, sum= out[15], carry= carry15);
}

An Incrementer is designed to add 1 to a given number. Although, the x + 1 operation can be realized with the general-purpose Adder chip, a dedicated Incrementer chip can do it more efficiently.
Chip name Inc16
Input in[16]
Output out[16]
Function out = in + 1
Comment The overflow bit is ignored. 
/**
* 16-bit incrementer:
* out = in + 1
*/

CHIP Inc16 {

IN in[16];

OUT out[16];

PARTS:

Add16(a = in, b[0] = true, b[1..15] = false, out = out);

}

The Arithmetic logic unit (ALU) is a chip designed to compute a set of arithmetic and logic operations. Unlike the generic chips discussed so far, the ALU described below is specific to the Hack computer:

x y zx nx zy ny f no out Description
0 y 1 0 1 0 1 0 0 0 (constant zero)
1 y 1 1 1 1 1 1 1 1 (constant one)
-1 y 1 1 1 0 1 0 -1 -1 (constant minus one)
x y 0 0 1 1 0 0 x x
x y 1 1 0 0 0 0 y y
x y 0 0 1 1 0 1 ¬x NOT x
x y 1 1 0 0 0 1 ¬y NOT y
x y 0 0 1 1 1 1 -x -x
x y 1 1 0 0 1 1 -y -y
x y 0 1 1 1 1 1 x+1 x + 1
x y 1 1 0 1 1 1 y+1 y + 1
x y 0 0 1 1 1 0 x-1 x - 1
x y 1 1 0 0 1 0 y-1 y - 1
x y 0 0 0 0 1 0 x+y x + y
x y 0 1 0 0 1 1 x-y x - y
x y 0 0 0 1 1 1 y-x y - x
x y 0 0 0 0 0 0 x&y x AND y
x y 0 1 0 1 0 1 x|y x OR y

The Hack ALU operates on two $16$-bit two's complement integers denoted x and y, an on six $1$-bit inputs, called control bits. The control bits "tell" the ALU which function to compute. Each control bit effects a standalone conditional micro-action:

1. if (zx) then x = 0 else x = x

2. if (nx) then x = !x else x = x

3. if (zy) then y = 0 else y = y

4. if (ny) then y = !y else y = y

5. if (f) then out = x + y else out = x and y

6. if (no) then out = !out else out = out

It may be instructive to describe the thought process that led to the design of this particular ALU. First, we made a list of all the primitive operations that we wanted our computer to be able to perform. Next, we used backward reasoning to figure out how x, y, and out can be manipulated in binary fashion in order to carry out the desired operations. These processing requirements, along with our objective to keep the ALU logic as simple as possible, have led to the design decision to use six control bits, each associated with a straightforward binary operation.

/**

* ALU (Arithmetic Logic Unit):

* Computes out = one of the following functions:

* 0, 1, -1,

* x, y, !x, !y, -x, -y,

* x + 1, y + 1, x - 1, y - 1,

* x + y, x - y, y - x,

* x & y, x | y

* on the 16-bit inputs x, y,

* according to the input bits zx, nx, zy, ny, f, no.

* In addition, computes the two output bits:

* if (out == 0) zr = 1, else zr = 0

* if (out < 0) ng = 1, else ng = 0

*/

// Implementation: Manipulates the x and y inputs

// and operates on the resulting values, as follows:

// if (zx == 1) sets x = 0 // 16-bit constant

// if (nx == 1) sets x = !x // bitwise not

// if (zy == 1) sets y = 0 // 16-bit constant

// if (ny == 1) sets y = !y // bitwise not

// if (f == 1) sets out = x + y // integer 2's complement addition

// if (f == 0) sets out = x & y // bitwise and

// if (no == 1) sets out = !out // bitwise not


CHIP ALU {

IN

x[16], y[16], // 16-bit inputs

zx, // zero the x input?

nx, // negate the x input?

zy, // zero the y input?

ny, // negate the y input?

f, // compute (out = x + y) or (out = x & y)?

no; // negate the out output?

OUT

out[16], // 16-bit output

zr, // if (out == 0) equals 1, else 0

ng; // if (out < 0) equals 1, else 0

  

PARTS:

// x's pre-processing

Mux16(a= x, sel= zx, out= x1);

Not16(in= x1, out= x1Negated);

Mux16(a= x1, b= x1Negated, sel= nx, out= x2);

  

// y's pre-processing

Mux16(a= y, sel= zy, out= y1);

Not16(in= y1, out= y1Negated);

Mux16(a= y1, b= y1Negated, sel= ny, out= y2);

  

// function

Add16(a = x2, b = y2, out = summed);

And16(a = x2, b = y2, out = andded);

Mux16(a= andded, b= summed, sel= f, out= out1);

  

// output post-processing

Not16(in= out1, out= out1Negated);

Mux16(a= out1, b= out1Negated, sel= no, out= out, out[15]= outFirst, out[0..7]= outLeft, out[8..15]= outRight);

  

// ng status bit

And(a= true, b= outFirst, out=ng);

  

// zr status bit

Or8Way(in= outLeft, out= zrLeft);

Or8Way(in= outRight, out= zrRight);

Or(a= zrLeft, b= zrRight, out= zrLeftOrZrRight);

Not(in= zrLeftOrZrRight, out= zr);

}

Chapter 3: Memory

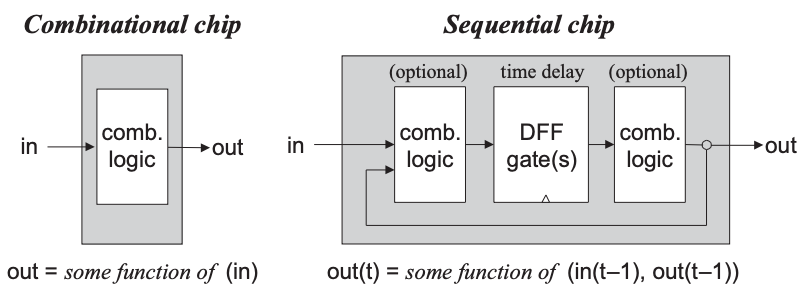
There are two types of chips:

  1. Combinational chips compute functions that depend solely on combinations of their input values. They cannot maintain state. All the chips built thus far are combinational chips.
  2. Sequential chips compute functions that depend on both their input values and their previous state. They have "memory" and can preserve data over time.

A flip-flop is a basic building block of sequential chips. It has two stable states and can be used to store state information.

A flip-flop encapsulates the intricate art of synchronization, clocking, and feedback loops that are essential for building sequential chips.

Using these flip-flops as elementary building blocks, we will specify and build all the memory devices employed by a typical modern computer: registers, RAMs, and counters.

This effort will complete the construction of the chip set needed to build an entire computer.

The act of "remembering something" is inherently time-dependent: You remember now what has been committed to memory before. Thus, in order to build chips that "remember" information, we must first develop some standard means for representing the progression of time.

In most computers, the progression of time is regulated by a clock signal. This signal oscillates between two values, 0 (called low/tick) and 1 (called high/tock), at a regular pace.

The clock hardware implementation is usually an oscillator that generates a square wave. The frequency of the clock signal is measured in Hertz (Hz), which is the number of oscillations per second.

Clock signal Image source

The elapsed time between the beginning of a "tick" and the end of a subsequent "tock" is called a clock cycle.

The clock is used to synchronize the sequential chips. Using the hardware’s circuitry, this signal is simultaneously broadcast to every sequential chip throughout the computer platform.

There are several variants of a flip-flop. We use a variant called the data flip-flop (DFF).

A DFF is a simple memory element that stores a single bit. It has a data input in, a clock input load, and an output out. When the clock input is 1, the flip-flop copies the value of the data input to its output. When the clock input is 0, the flip-flop holds its previous value.

Taken together, both inputs enables the DFF to implement the behavior out(t) = in(t-1), where t is the current clock cycle. In other words, the DFF outputs the input value from the previous clock cycle.

DFF
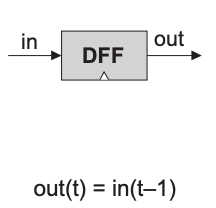
Chip name DFF
Input in, load
Output out
Function out(t) = in(t-1)
Comment This clocked gate has a built-in implementation and thus there is no need to implement it.

[...] When the clock input is 1, the flip-flop copies the value of the data input to its output. When the clock input is 0, the flip-flop holds its previous value.

Actually, what we described previously is a latch: which is level-triggered.

A DFF is edge-triggered. Our DFF will be rising edge-triggered, meaning it only copies the in data input when the clock signal transitions from 0 to 1.

All DFFs in a computer are connected to the same clock signal.

This reliable and predictable behavior of DFFs is crucial for data synchronization across the computer platform. There are physical delays in the propagation of signals through the computer’s hardware, e.g. It takes some time for the input into the ALU to stabilize and for the ALU to compute its output.

We solve this problem by using discrete time:

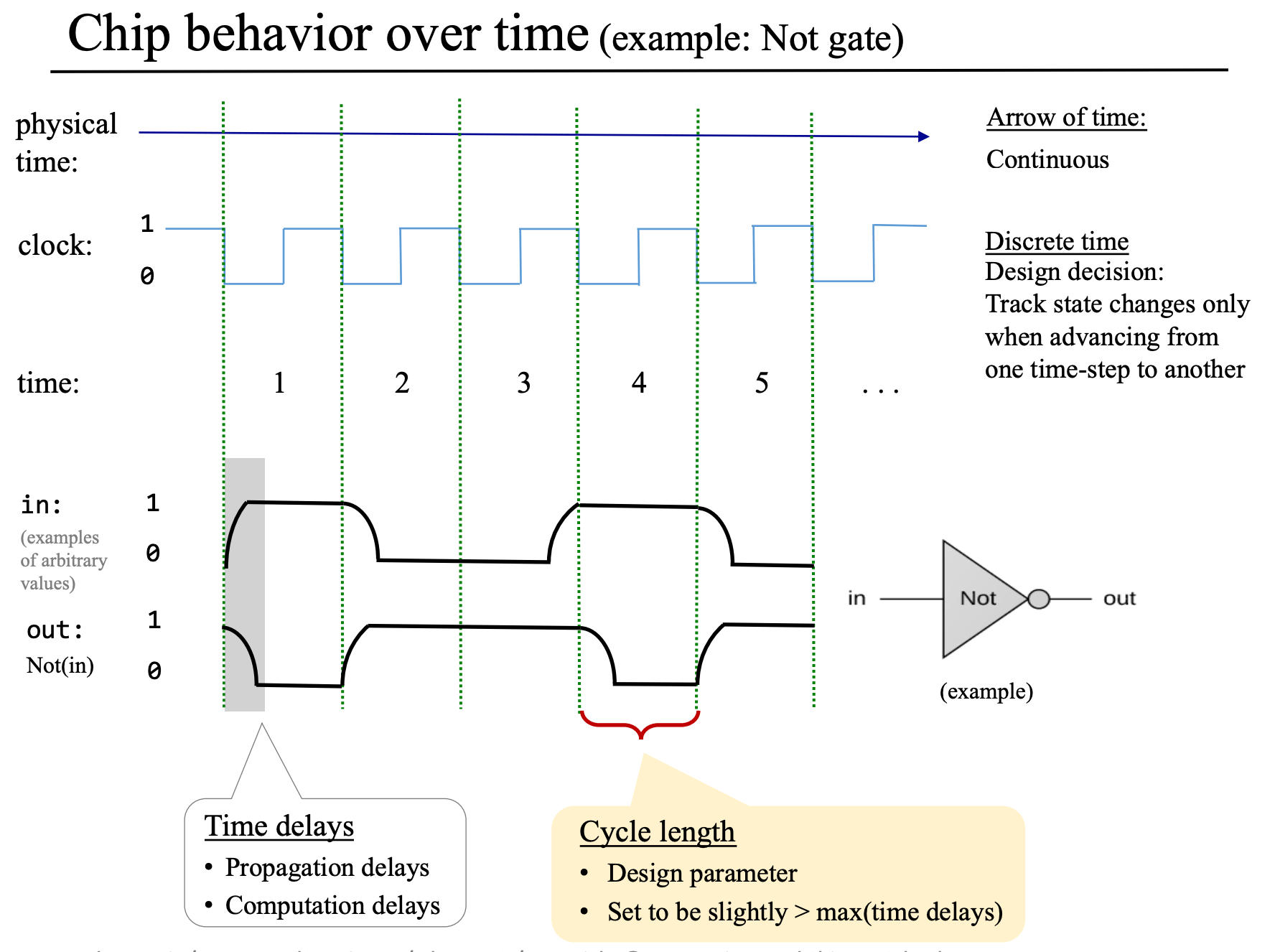
Discrete time

A register is a storage device that can "store" or "remember" a value over time, implementing the classical storage behavior out = out(t-1).

A DFF, on the other hand, can only output its previous input, namely, out = in(t-1). We can build a register from a DFF, however, we must consider the following:

  1. The rules of chip design dictate that internal pins must have a fan-in of 1, meaning that they can be fed from a single source only.
  2. We need to be able to specify when to read from the DFF and when to write to it.

A natural way to build our register is to use a multiplexor: the "select bit" of the multiplexor becomes the "load bit" of the overall register chip:

If we want the register to start storing a new value, we can put this value in the in input and set the load bit to 1; if we want the register to keep storing its internal value until further notice, we can set the load bit to 0.

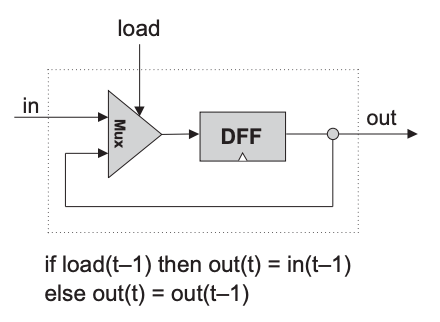
Register
Chip name Bit or Binary cell (Single bit register)
Input in, load
Output out
Function if (load(t-1) == 1) out(t) = in(t-1) else out(t) = out(t-1) 
CHIP Bit {
    IN in, load;
    OUT out;

    PARTS:
    DFF(in= dffIn, out= dffOut, out= out);
    Mux(a= dffOut, b= in, sel= load, out= dffIn);
}

A multi-bit register of width w can be constructed from an array of w 1-bit registers. The basic design parameter of such a register is its width — the number of bits that it holds — e.g., 16, 32, or 64. The multi-bit contents of such registers are typically referred to as words.
Chip name Register
Input in[16], load
Output out[16]
Function if (load(t-1) == 1) out(t) = in(t-1) else out(t) = out(t-1) 
CHIP Register {
    IN in[16], load;
    OUT out[16];

    PARTS:
    Bit(in= in[0], load= load, out= out[0]);
    Bit(in= in[1], load= load, out= out[1]);
    Bit(in= in[2], load= load, out= out[2]);
    Bit(in= in[3], load= load, out= out[3]);
    Bit(in= in[4], load= load, out= out[4]);
    Bit(in= in[5], load= load, out= out[5]);
    Bit(in= in[6], load= load, out= out[6]);
    Bit(in= in[7], load= load, out= out[7]);
    Bit(in= in[8], load= load, out= out[8]);
    Bit(in= in[9], load= load, out= out[9]);
    Bit(in= in[10], load= load, out= out[10]);
    Bit(in= in[11], load= load, out= out[11]);
    Bit(in= in[12], load= load, out= out[12]);
    Bit(in= in[13], load= load, out= out[13]);
    Bit(in= in[14], load= load, out= out[14]);
    Bit(in= in[15], load= load, out= out[15]);
}

A RAM chip (aka direct access memory unit) is a sequential chip that can store multiple data words. Each word is stored in a register, and the registers are indexed by an address.

RAM

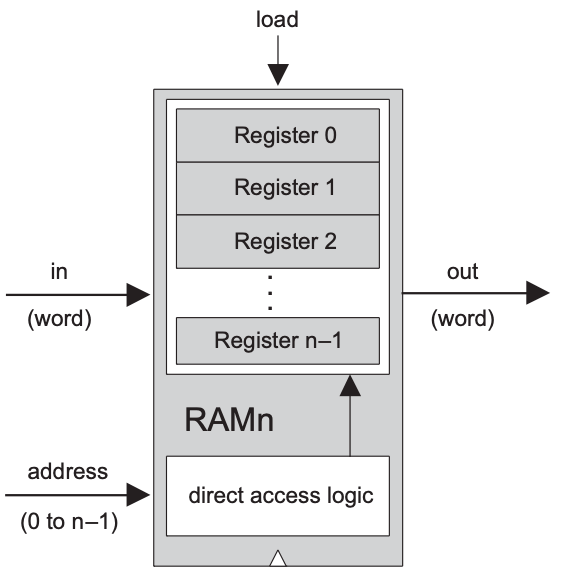
The term random access memory derives from the requirement that any randomly chosen word in the memory — irrespective of its physical location — be accessed directly, in equal speed.

This requirement can be satisfied as follows:

In sum, a classical RAM device accepts three inputs: a data input, an address input, and a load bit. The address specifies which RAM register should be accessed in the current time unit.

In the case of a read operation (load=0), the RAM’s output immediately emits the value of the selected register.

In the case of a write operation (load=1), the selected memory register commits to the input value in the next time unit, at which point the RAM’s output will start emitting it.

The basic design parameters of a RAM device are:

  1. Its data width — the width of each one of its words, and
  2. Its size — the number of words in the RAM.
Chip name RAMn
Input in[16], address[k], load
Output out[16]
Function out(t) = RAM[address(t)](t)
if (load(t-1) == 1) then RAM[address(t-1)](t) = in(t-1)
Comment k=log2nk = log_2{n} and we will build RAM8( n=8n=8 ),RAM64( n=64n=64 ),RAM512( n=512n=512 ),RAM4K( n=4096n=4096 ),RAM16K( n=16384n=16384 ), 
CHIP RAM8 {
    IN in[16], load, address[3];
    OUT out[16];

    PARTS:
    CHIP RAM8 {
    IN in[16], load, address[3];
    OUT out[16];

    PARTS:
    DMux8Way(in= load, sel= address, a= loadA, b= loadB, c= loadC, d= loadD, e= loadE, f= loadF, g= loadG, h= loadH);
    Register(in= in, load= loadA, out= out1);
    Register(in= in, load= loadB, out= out2);
    Register(in= in, load= loadC, out= out3);
    Register(in= in, load= loadD, out= out4);
    Register(in= in, load= loadE, out= out5);
    Register(in= in, load= loadF, out= out6);
    Register(in= in, load= loadG, out= out7);
    Register(in= in, load= loadH, out= out8);
    Mux8Way16(a= out1, b= out2, c= out3, d= out4, e= out5, f= out6, g= out7, h= out8, sel= address, out= out);
}
}

CHIP RAM64 {
    IN in[16], load, address[6];
    OUT out[16];

    PARTS:
    DMux8Way(in= load, sel= address[3..5], a= load1, b= load2, c= load3, d= load4, e= load5, f= load6, g= load7, h= load8);
    RAM8(in= in, load= load1, address= address[0..2], out= out1);
    RAM8(in= in, load= load2, address= address[0..2], out= out2);
    RAM8(in= in, load= load3, address= address[0..2], out= out3);
    RAM8(in= in, load= load4, address= address[0..2], out= out4);
    RAM8(in= in, load= load5, address= address[0..2], out= out5);
    RAM8(in= in, load= load6, address= address[0..2], out= out6);
    RAM8(in= in, load= load7, address= address[0..2], out= out7);
    RAM8(in= in, load= load8, address= address[0..2], out= out8);
    Mux8Way16(a= out1, b= out2, c= out3, d= out4, e= out5, f= out6, g= out7, h= out8, sel= address[3..5], out= out);
}

CHIP RAM512 {
    IN in[16], load, address[9];
    OUT out[16];

    PARTS:
    DMux8Way(in= load, sel= address[6..8], a= load1, b= load2, c= load3, d= load4, e= load5, f= load6, g= load7, h= load8);
    RAM64(in= in, load= load1, address= address[0..5], out= out1);
    RAM64(in= in, load= load2, address= address[0..5], out= out2);
    RAM64(in= in, load= load3, address= address[0..5], out= out3);
    RAM64(in= in, load= load4, address= address[0..5], out= out4);
    RAM64(in= in, load= load5, address= address[0..5], out= out5);
    RAM64(in= in, load= load6, address= address[0..5], out= out6);
    RAM64(in= in, load= load7, address= address[0..5], out= out7);
    RAM64(in= in, load= load8, address= address[0..5], out= out8);
    Mux8Way16(a= out1, b= out2, c= out3, d= out4, e= out5, f= out6, g= out7, h= out8, sel= address[6..8], out= out);

}

CHIP RAM4K {
    IN in[16], load, address[12];
    OUT out[16];

    PARTS:
    DMux8Way(in= load, sel= address[9..11], a= load1, b= load2, c= load3, d= load4, e= load5, f= load6, g= load7, h= load8);
    RAM512(in= in, load= load1, address= address[0..8], out= out1);
    RAM512(in= in, load= load2, address= address[0..8], out= out2);
    RAM512(in= in, load= load3, address= address[0..8], out= out3);
    RAM512(in= in, load= load4, address= address[0..8], out= out4);
    RAM512(in= in, load= load5, address= address[0..8], out= out5);
    RAM512(in= in, load= load6, address= address[0..8], out= out6);
    RAM512(in= in, load= load7, address= address[0..8], out= out7);
    RAM512(in= in, load= load8, address= address[0..8], out= out8);
    Mux8Way16(a= out1, b= out2, c= out3, d= out4, e= out5, f= out6, g= out7, h= out8, sel= address[9..11], out= out);

}

CHIP RAM16K {
    IN in[16], load, address[14];
    OUT out[16];

    PARTS:
    DMux8Way(in= load, sel= address[11..13], a= load1, b= load2, c= load3, d= load4, e= load5, f= load6, g= load7, h= load8);
    RAM4K(in= in, load= load1, address= address[0..11], out= out1);
    RAM4K(in= in, load= load2, address= address[0..11], out= out2);
    RAM4K(in= in, load= load3, address= address[0..11], out= out3);
    RAM4K(in= in, load= load4, address= address[0..11], out= out4);
    RAM4K(in= in, load= load5, address= address[0..11], out= out5);
    RAM4K(in= in, load= load6, address= address[0..11], out= out6);
    RAM4K(in= in, load= load7, address= address[0..11], out= out7);
    RAM4K(in= in, load= load8, address= address[0..11], out= out8);
    Mux8Way16(a= out1, b= out2, c= out3, d= out4, e= out5, f= out6, g= out7, h= out8, sel= address[11..13], out= out);
    
}

A counter is a sequential chip whose state is an integer number that increments every time unit, effecting the function out = out(t - 1) + c, where c is typically 1.

A counter chip can be implemented by combining the input/output logic of a standard register with the combinatorial logic for adding a constant.

Typically, the counter will have to be equipped with some additional functionality, such as possibilities for resetting the count to zero, loading a new counting base, or decrementing instead of incrementing.
Chip name Counter
Input in[16], load, inc, reset
Output out[16]
Function if (reset(t-1) == 1) then out(t) = 0
else if (load(t-1) == 1) then out(t) = in(t-1)
else if (inc(t-1) == 1) then out(t) = out(t-1) + 1
else out(t) = out(t-1)		 
CHIP PC {
    IN in[16], reset, load, inc;
    OUT out[16];
    
    PARTS:
    Register(in= inRegister, load= true, out= outRegister, out= out);
    Inc16(in= outRegister, out= outInc);
    Mux16(a= outRegister, b= outInc, sel= inc, out= out1);
    Mux16(a= out1, b= in, sel= load, out= out2);
    Mux16(a= out2, b= false, sel= reset, out= inRegister);
}

Simply stated, a sequential chip is a chip that embeds one or more DFF gates, either directly or indirectly.

Sequential chip

Chapter 4: Machine Language

A machine language is an agreed-upon formalism, designed to code low-level programs as series of machine instructions. The primary goals of a machine language's design are:

  1. Direct execution in, and
  2. Total control of, a given hardware platform.

A machine language is the fine line where hardware and software meet: it can be considered as both a programming tool and an integral part of the hardware platform.

This chapter only focuses on the machine language and leaves the hardware details to the next chapter. To give a general description of machine languages, it's sufficient to only use three main hardware abstractions:

  1. Processor: The processor, normally called the CPU (Central Processing Unit), is a device capable of performing a fixed set of elementary operations. These typically include:

    The operands of these operations and their results/output are binary values that are read and stored in registers or selected memory locations.

  2. Memory: The term memory refers loosely to the collection of hardware devices that store data and instructions in a computer.

  3. Set of registers: Memory access is a relatively slow operation, requiring long instruction formats. For this reason, most processors are equipped with several registers, each capable of holding a single value, allowing the processor to manipulate data and instructions quickly.

A machine language is a series of coded instructions. For example, an instruction in a 16-bit computer may be 1010001100011001. In order to figure out what this instruction means, we must know the instruction set of the underlying hardware platform. For example, the language, may be such that each instruction consists of four 4-bit fields: The left-most field codes a CPU operation, and the remaining three fields code the operation's operands.

Since binary codes are rather cryptic, machine languages are normally specified using both binary codes and symbolic mnemonics. A mnemonic is a short, easy-to-remember name for a binary code. For example, the binary code 1010001100011001 may be associated with the mnemonic ADD R1, R2, R3.

Hence, a machine language instruction can be specified either directly using binary codes or indirectly using symbolic mnemonics.

We can take the symbolic abstraction one step further, and create a programming language that allows the creation of programs using symbolic commands rather than binary instructions. This programming language is called an assembly language. And the symbolic mnemonics are just a component of the assembly language, specifically the symbols that represent machine instructions.

The Hack computer is a von Neumann platform. It's a simple computer with a $16$-bit architecture which has:

  1. A CPU
  2. A read-only memory (ROM) that stores the computer instructions. It is 16$-bit wide and have a $15$-bit address space (i.e. it can hold $32K (2^{15}) $16$-bit instructions).
  3. A random access memory (RAM) that stores the computer data. It is also $16$-bit wide and have a $15$-bit address space.
  4. Two memory-mapped I/O devices: a screen and a keyboard.
  5. A $16$-bit instruction set.
  6. Two $16$-bit registers called A and D. These registers can be manipulated explicitly by arithmetic and logical instructions (e.g. D=A+1, A=D&A). The D register is used solely to store data values; while the A register is used to both store data values and memory addresses. So, depending on the context, the contents of A can be interpreted as:

Why do we overload the A register with so many roles? Since Hack instructions are 16-bit wide, and since addresses are specified using 15-bits, it's impossible to pack both an operation code and an address in one instruction. Thus, the syntax of the Hack language mandates that memory access instructions operate on an implicit memory location labeled M, for example D=M+1. In order to resolve this address, the convention is that M always refers to the memory word whose address is the current value of the A register. That is M is a synonym for RAM[A]. This implies, we must first load the address into the A register before we can access the memory word at that address.

This also applies to instruction memory access. To jump to a specific instruction, we must first load the address of that instruction into the A register.

In a nutshell, the A register's value is interpreted based on how it is used in subsequent instructions.

An alternative solution would be to have more registers, but this would have increased the complexity of the hardware.

The Hack language consists of two generic instructions:

  1. An address instruction (A-instruction) and
  2. A compute instruction (C-instruction).

The A-instruction is used to set the A register to a $15$-bit value:

A-instruction's symbolic representation: @value (where value is a non-negative decimal number or a symbol referring to such a number). A-instruction's binary representation: 0value (where value is a $15$-bit binary number).

The leftmost bit is the A-instruction marker bit (aka opcode), which is always set to 0.

The A-instruction is used for three different purposes:

  1. It provides the only way to enter a constant into the computer under program control.
  2. It sets the stage for a subsequent C-instruction designed to access a specific location in the data memory.
  3. It sets the stage for a subsequent C-instruction designed to jump to a specific location in the instruction memory.

The C-instruction is used to perform a computation. The instruction code is a specification that answers three questions:

  1. What to compute?
  2. Where to store the computed value?
  3. What to do next?

C-instruction's symbolic representation: dest=comp;jump (where dest is the destination register, comp is the computation, and jump is the jump condition). Both dest= and ;jump are optional. C-instruction's binary representation: 1 1 1 a c_1 c_2 c_3 c_4 c_5 c_6 d_1 d_2 d_3 j_1 j_2 j_3 (where a_n & c_n specify the comp component; d_n specifies the dest component, and j_n specifies the jump component).

The leftmost bit is the C-instruction marker bit (aka opcode), which is always set to 1. The next wo bits are not used and are set to 1.

The dest component of the C-instruction specifies where to store the computed value (the ALU output).

The first and second bits specify whether to store the computed value in the A register and in the D register, respectively. The third bit specifies whether to store the computed value in the data memory location specified by the A register.

d1 d2 d3 dest mnemonic Destination (where to store the computed value)
0 0 0 null Do not store the computed value
0 0 1 M Store the computed value in the data memory
0 1 0 D Store the computed value in the D register
0 1 1 MD Store the computed value in the D register and in the data memory
1 0 0 A Store the computed value in the A register
1 0 1 AM Store the computed value in the A register and in the data memory
1 1 0 AD Store the computed value in the A register and in the D register
1 1 1 AMD Store the computed value in the A register, in the D register, and in the data memory

The comp component of the C-instruction specifies what the ALU should compute. We can compute a fixed set of functions on the D, A, and M registers. The a-bit specifies whether the A register or the M register should be used as the ALU's input. And the six c-bits specifies the function to be computed. All 7$-bit comprise the `comp` field. While this $7$-bit field can specify $128 different possible operations, only 2828 are used in the Hack language.

(when a=0) comp mnemonic c1 c2 c3 c4 c5 c6 (when a=1) comp mnemonic
0 1 0 1 0 1 0
1 1 1 1 1 1 1
-1 1 1 1 0 1 0
D 0 0 1 1 0 0
A 1 1 0 0 0 0 M
!D 0 0 1 1 0 1
!A 1 1 0 0 0 1 !M
-D 0 0 1 1 1 1
-A 1 1 0 0 1 1 -M
D+1 0 1 1 1 1 1
A+1 1 1 0 1 1 1 M+1
D-1 0 0 1 1 1 0
A-1 1 1 0 0 1 0 M-1
D+A 0 0 0 0 1 0 D+M
D-A 0 1 0 0 1 1 D-M
A-D 0 0 0 1 1 1 M-D
D&A 0 0 0 0 0 0 D&M
D|A 0 1 0 1 0 1 D|M

The jump component of the C-instruction specifies a jump condition, namely, which command to fetch and execute next. Whether a not a jump should actually materialize depends on the three j-bits of the jump component and the ALU's output value. It is a 3$-bit field that can specify one of $8 different jump conditions.

j1 (out < 0) j2 (out = 0) j3 (out > 0) jump mnemonic Effect
0 0 0 null No jump (this is the default, it simply proceeds to the next instruction)
0 0 1 JGT Jump if out > 0
0 1 0 JEQ Jump if out = 0
0 1 1 JGE Jump if out >= 0
1 0 0 JLT Jump if out < 0
1 0 1 JNE Jump if out != 0
1 1 0 JLE Jump if out <= 0
1 1 1 JMP Jump unconditionally

The JMP is used as 0;JMP. This is because the C-instruction syntax requires that we always effect some computation, we instruct the ALU to compute 00 (an arbitrary choice), which is ignored.

Example: We want the computer to increment the value of DataMemory[7] by 11 and to also store the result in the D register. This can be achieved with the following instructions:

 0000 0000 0000 0111 // @7
 1111 1101 1101 1000 // MD=M+1

Assembly commands can refer to memory addresses using either constants or symbols. Symbols are introduced into assembly programs in the following three ways:

  1. Predefined symbols: A subset of RAM addresses have predefined symbols:
  2. Label symbols: These are user-defined symbols serve to label destinations of goto commands. They are declared by the pseudo-command (Xxx). This directive defines the symbol Xxx to refer to the ROM address holding the next command in the program.
  3. Variable symbols: Any user-defined symbol Xxx that appears in an assembly program without being predefined or declared as a label is treated as a variable. The assembler allocates a unique RAM address for each appearance of such a symbol and replaces the symbol with its RAM address in the assembly program. The instruction is of the form @value, where value is a $15$-bit constant.

The Hack platform can be connected to two peripheral devices: a screen and a keyboard. Both devices interact with the computer platform through memory maps. This means that drawing pixels on the screen is achieved by writing binary values into a memory segment associated with the screen. Likewise, listening to the keyboard is done by reading a memory location associated with the keyboard. The physical I/O devices and their memory maps are synchronized via continuous refresh loops.

The Hack computer includes a black-and-white screen organized as 256256 rows of 512512 pixels per row. The screen’s contents are represented by an 8K memory map that starts at RAM address 1638416384 ($0x4000$). Each row in the physical screen, starting at the screen’s top left corner, is represented in the RAM by 3232 consecutive $16$-bit words. Thus, the pixel at row r from the top and column c from the left is mapped on the c%16 bit (counting from LSB to MSB) of the word located at RAM[16384 + r * 32 + c/16]. To write or read a pixel of the physical screen, one reads or writes the corresponding bit in the RAM-resident memory map (1 = black, 0 = white).

Example:

// Draw a single black dot at the screen's top left corner:
@SCREEN // Set the A register to point to the memory
       // word that is mapped to the 16 left-most
      // pixels of the top row of the screen.
M=1 // Blacken the left-most pixel.

The Hack computer interfaces with the physical keyboard via a single-word memory map located in RAM address 2457624576 ($0x6000$). Whenever a key is pressed on the physical keyboard, its $16$-bit ASCII code appears in RAM[24576]. When no key is pressed, the code 0 appears in this location. In addition to the usual ASCII codes, the Hack keyboard recognizes the keys shown below.

Key pressed Code
newline 128
backspace 129
left arrow 130
up arrow 131
right arrow 132
down arrow 133
home 134
end 135
page up 136
page down 137
insert 138
delete 139
esc 140
f1-f2 141-152

Chapter 5: Computer Architecture

The computer is based on a fixed hardware platform, capable of executing a fixed repertoire of simple instructions. However, these instructions can be combined like building blocks, yielding arbitrarily sophisticated programs.

The von Neumann architecture, shown below, is based on a central processing unit (CPU), interacting with a memory device, receiving data from some input device, and sending data to some output device.

At the heart of this architecture lies the stored program concept: The computer's memory stores both the data that the computer manipulates and the instructions that tell the computer what to do.

Von Neumann architecture

A related stored program computer architecture is the Harvard architecture, which physically separates the memory devices used for storing data and instructions.

Harvard architecture

The CPU operation can be described as a repeated loop (aka fetch-decode-execute cycle):

  1. Fetches (i.e, reads) a binary machine instruction from a selected register in the instruction memory
  2. Decodes it
  3. Executes the specified instruction
  4. And figures out which instruction to fetch and execute next.

(3) and (4) are based on the fetched instruction which tells the CPU:

The CPU executes these tasks using three main hardware elements:

The first two elements were already introduced in the previous chapters.

A computer instruction is represented as a binary code, typically 16, 32, or 64 bits wide. Before such an instruction can be executed, it must be decoded, and the information embedded in it must be used to signal various hardware devices (ALU, registers, memory) how to execute the instruction.

The instruction decoding is done by some control unit, which is also responsible for figuring out which instruction to fetch and execute next.

The set of registers used by the Hack computer are:

The Hack computer is a 16-bit machine based on the Harvard architecture, designed to execute instructions written in the Hack machine language.

The Hack CPU interface:

/**
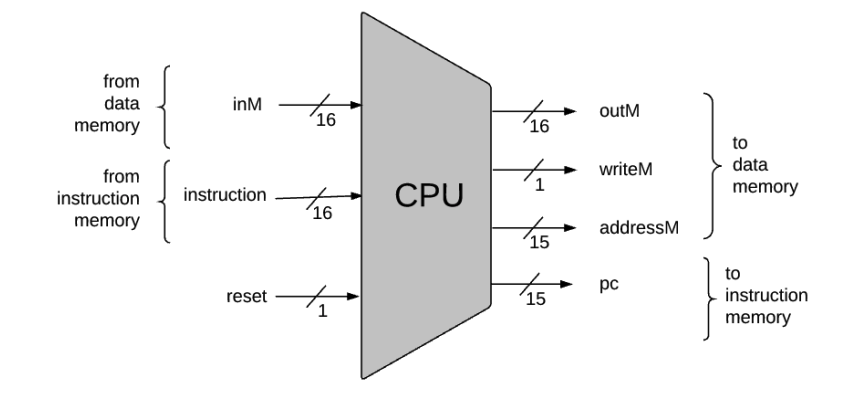
	CHIP	CPU
	
	IN
	    instruction[16],	//	Instruction	to	execute.
	    inM[16],			//	Value	of	Mem[A],	the	instruction’s	M	input
	    reset;				//	Signals	whether	to	continue	executing	the	current	program	(reset==0)	or	restart	the	current	program	(reset==1).
	    
	OUT
	    outM[16],			//	Value	to	write	to	Mem[addressM],	the	instruction’s	M	output
	    addressM[15],		//	In	which	address	to	write?
	    writeM,				//	Write	to	the	Memory?
	    pc[15];				//	address	of	next	instruction

Hack CPU

Key points:

The Hack instruction memory interface:

CHIP	ROM32K

    IN
        address[15];
    
    OUT
        out[16];

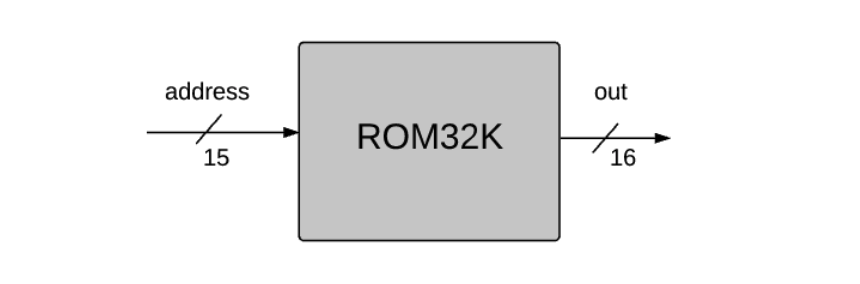
Hack instruction memory

Key points:

The Hack data memory interface:

CHIP Memory

    IN
        in[16],	load,	address[15];
    
    OUT
        out[16];

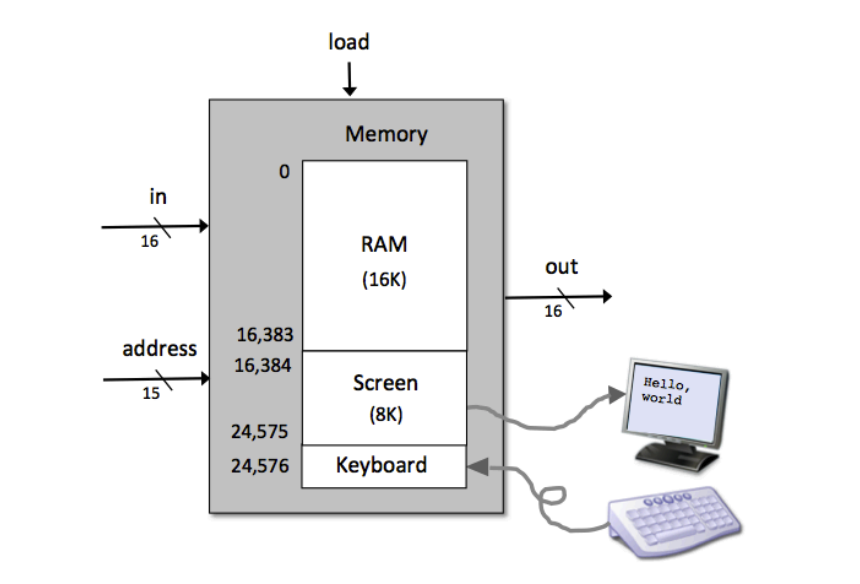
Hack data memory

Key points:

The interface of the topmost chip in the Hack hardware platform, named Computer:

CHIP Computer

    IN
        reset;

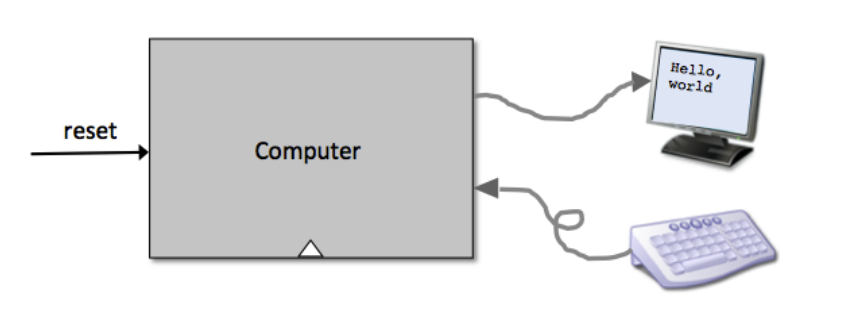
Hack computer

Key points:

The Hack keyboard chip interface:

CHIP Keyboard

    OUT
        out[16]; //	The	scan-code	of	the	pressed	key, or	0	if	no	key	is	currently	pressed.

Keypoint:

The Hack screen chip interface:

CHIP Screen

    IN
        in[16], //	what	to	write
        address[13]; //	where	to	write	(or	read)
        load, // write-enable	bit
    
    OUT
        out[16]; //	Screen	value	at	the	given	address

Keypoint:

All the chips needed to build the Hack CPU have been built in the previous chapters, the key question is how to arrange and connect them in a way that effects the desired CPU operation.

The architecture shown below is used to perform three classical CPU tasks:

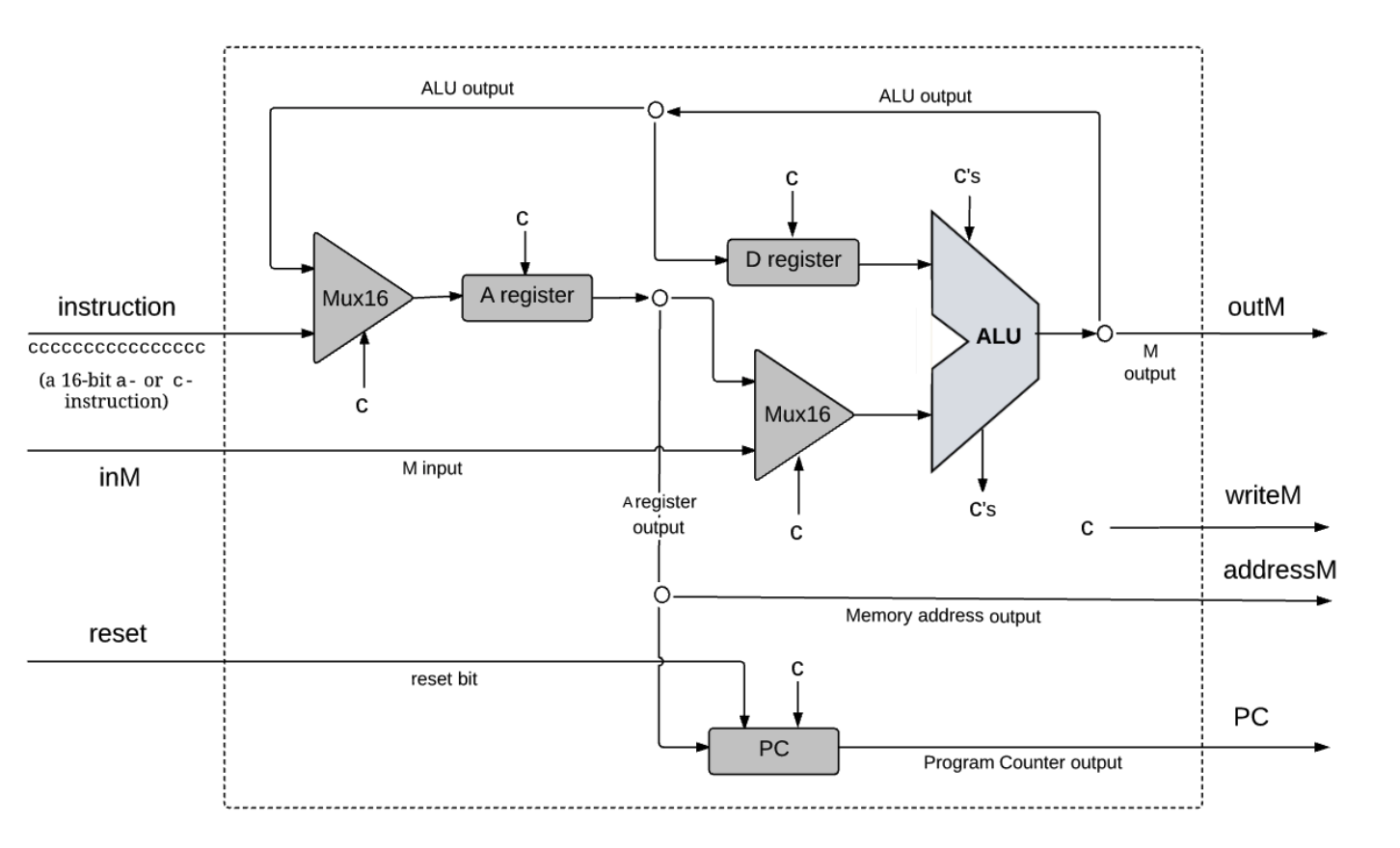Hack CPU architecture Every c symbol entering a chip-part stands for some control bit, extracted from the instruction. In the case of the ALU, the c's input stands for the 6 control bits that instruct the ALU what to compute, and the c's output stands for its zr and ng outputs. Taken together, the distributed behaviors that these control bits effect throughout the CPU architecture end up executing the instruction.

// This file is part of www.nand2tetris.org
// and the book "The Elements of Computing Systems"
// by Nisan and Schocken, MIT Press.
// File name: projects/5/CPU.hdl
/**
 * The Hack Central Processing unit (CPU).
 * Parses the binary code in the instruction input and executes it according to the
 * Hack machine language specification. In the case of a C-instruction, computes the
 * function specified by the instruction. If the instruction specifies to read a memory
 * value, the inM input is expected to contain this value. If the instruction specifies
 * to write a value to the memory, sets the outM output to this value, sets the addressM
 * output to the target address, and asserts the writeM output (when writeM = 0, any
 * value may appear in outM).
 * If the reset input is 0, computes the address of the next instruction and sets the
 * pc output to that value. If the reset input is 1, sets pc to 0.
 * Note: The outM and writeM outputs are combinational: they are affected by the
 * instruction's execution during the current cycle. The addressM and pc outputs are
 * clocked: although they are affected by the instruction's execution, they commit to
 * their new values only in the next cycle.
 */
CHIP CPU {

    IN  inM[16],         // M value input  (M = contents of RAM[A])
        instruction[16], // Instruction for execution
        reset;           // Signals whether to re-start the current
                         // program (reset==1) or continue executing
                         // the current program (reset==0).

    OUT outM[16],        // M value output
        writeM,          // Write to M? 
        addressM[15],    // Address in data memory (of M)
        pc[15];          // address of next instruction

    PARTS:
    // Negate the opCode.
    Not(in= instruction[15], out= notOpCode);
    // If opCode == 0, we route the instruction into the A register. Else, we route the ALU input.
    Mux16(a= outputOfALU, b= instruction, sel= notOpCode, out= inputToA);
    // The A register is enabled for writing if we have an A-instruction or a C-instruction with the d_1 control bit asserted.
    Or(a= notOpCode, b= instruction[5], out= writeToA);
    ARegister(in= inputToA, load= writeToA, out= outputOfA, out[0..14]=addressM);

    // Only select M, if we have an C-instruction and the a-bit is asserted
    And(a= instruction[15], b= instruction[12], out= controlAOrM);
    Mux16(a= outputOfA, b= inM, sel= controlAOrM, out= AOrM);
    // Use the ALU.
    ALU(x= outputOfD, y= AOrM, zx= instruction[11], nx= instruction[10], zy= instruction[9], ny= instruction[8], f= instruction[7], no= instruction[6], out= outputOfALU, out = outM, zr= isAluOutputZero, ng= isAluOutputNegative);

    // Only write to the D register, if we have a C-instruction AND the d_2 bit is asserted.
    And(a= instruction[15], b= instruction[4], out= writeToD);
    DRegister(in= outputOfALU, load= writeToD, out= outputOfD);

    // Only set writeM to true, if we have a C-instruction and the d_1 bit is asserted.
    And(a= instruction[15], b= instruction[3], out= controlWriteM);
    Mux(a= false, b= true, sel= controlWriteM, out= writeM);

    // Derive if ALU output is positive (i.e, it's not negative or zero)
    Or(a= isAluOutputNegative, b= isAluOutputZero, out= isAluOutputNegativeOrZero);
    Not(in= isAluOutputNegativeOrZero, out= isAluOutputPositive);

    // Check j_1 against ALU output is negative bit.
    And(a= instruction[2], b= isAluOutputNegative, out= jumpCauseNegative);
    // Check j_2 against ALU output is zero bit.
    And(a= instruction[1], b= isAluOutputZero, out= jumpCauseZero);
    // Check j_3 against ALU output is positive bit.
    And(a= instruction[0], b= isAluOutputPositive, out= jumpCausePositive);
    
    // Combine: We jump if we have a C-instruction and any of the jump predicates matches.
    Or(a= jumpCauseNegative, b= jumpCauseZero, out= jumpIntermediate);
    Or(a= jumpIntermediate, b= jumpCausePositive, out= jumpIntermediate2);
    And(a= instruction[15], b= jumpIntermediate2, out= controlJump);

    PC(in= outputOfA, load= controlJump, inc= true, reset= reset, out[0..14]= pc);
}